Shapes

It is recommended to run the examples in this section in release mode, as the checks performed in debug mode can cause a significant slowdown.

Plotting

To plot a 2D shape, you must create a 2D canvas object, plot any shapes, and run the canvas. A simple example is shown

use algebraeon::drawing::canvas::Canvas;
use algebraeon::drawing::canvas2d::Canvas2D;
use algebraeon::drawing::canvas2d::MouseWheelZoomCamera;
use algebraeon::geometry::parse::parse_shape;

let shape = parse_shape(
    "Polygon((0, 0), (6, 0), (6, 6), (2, 3), (0, 4)) \\ Polygon((1, 1), (2, 1), (2, 2), (1, 3))",
);

let mut canvas = Canvas2D::new(Box::new(MouseWheelZoomCamera::new()));
canvas.plot(shape);
canvas.run();

It produces the following plot, in an interactive 2D viewer:

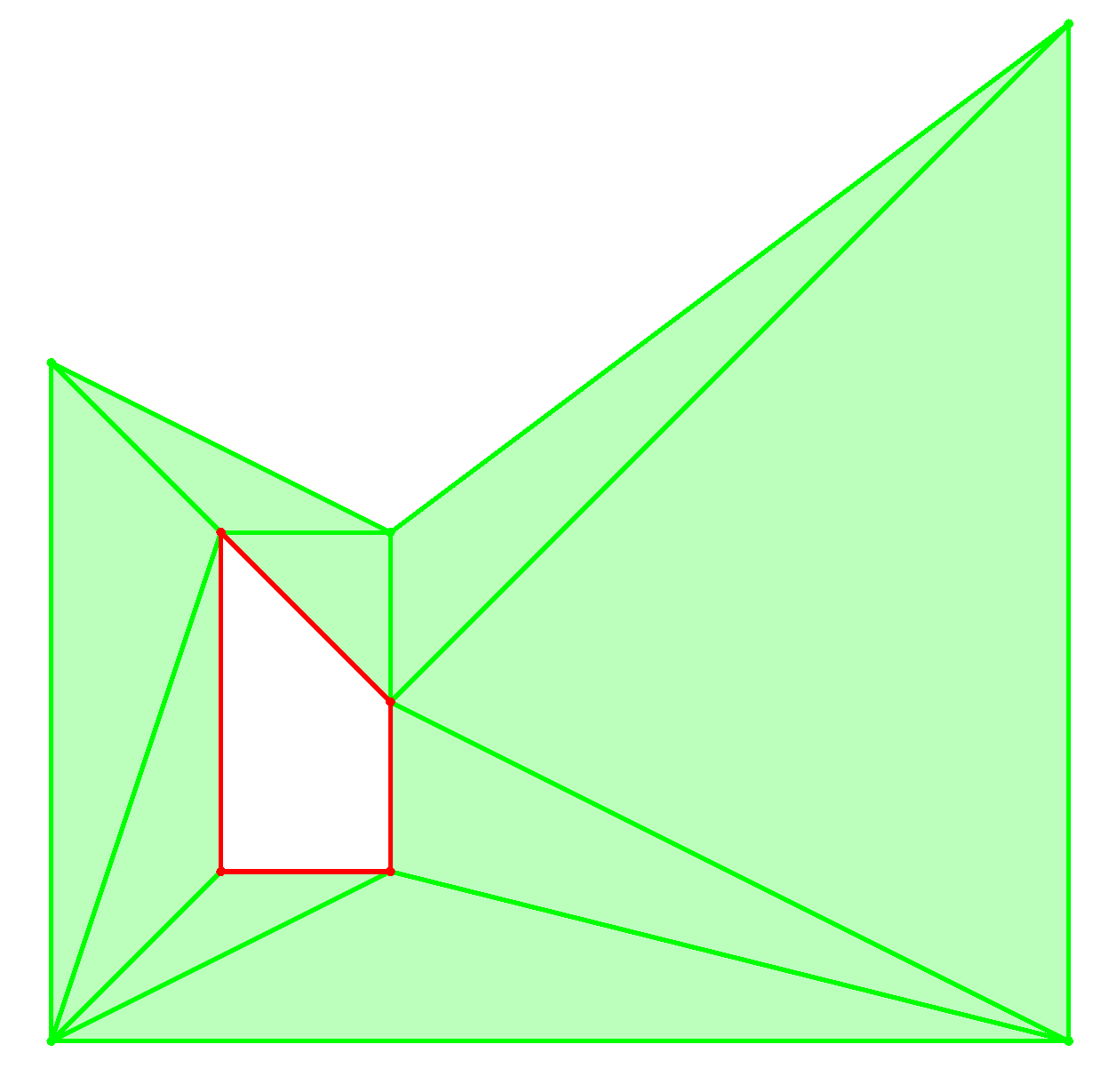
Green areas indicate points that are part of the shape. Red areas indicate boundary points that are not part of the shape.

Loading a Shape From a String

The supported syntax when loading a shape from a string:

• Point(<point>): A single point.
• Lines(<points>): The union of line segments connecting each consecutive pair of points in the list.
• Polygon(<points>): The closed polygon whose vertices are those given. Only works in 2D.
• PolygonInterior(<points>): The interior of the polygon whose vertices are those given. Only works in 2D.
• Loop(<points>): The union of line segments connecting each consecutive pair of points in the list, including the line segment connecting the first and last point.
• ConvexHull(<points>): The convex hull of the provided points.
• ConvexHullInterior(<points>): The interior of the convex hull of the provided points. The interior is taken with respect to the affine subspace spanned by the points.
• ConvexHullBoundary(<points>): The boundary of the convex hull of the provided points. The boundary is taken with respect to the affine subspace spanned by the points.
• ShapeA | ShapeB: The union of shapes.
• ShapeA & ShapeB: The intersection of shapes.
• ShapeA \ ShapeB: The difference of shapes.
• ShapeA + ShapeB: The Minkowski sum of shapes.